Выполнить умножение дробей. Как перемножить обыкновенную дробь с натуральным числом
Умножение целого числа на дробь – несложная задача. Но есть тонкости, в которых вы, наверняка, разбирались в школе, но с тех пор забыли.
Как умножить целое число на дробь – немного терминов
Если вы помните, что такое числитель, знаменатель и чем отличается правильная дробь от неправильной – пропустите этот абзац. Он для тех, кто совсем забыл теорию.
Числитель – это верхняя часть дроби – то, что делим. Знаменатель – нижняя. Это то, на что делим.
Правильная дробь та, у которой числитель меньше знаменателя. Неправильной называется дробь, у которой числитель больше или равен знаменателю.
Как умножить целое число на дробь
Правило умножения целого числа на дробь очень простое – умножаем числитель на целое, а знаменатель не трогаем. Например: два умножить на одну пятую – получаем две пятых. Четыре умножить на три шестнадцатых – получится двенадцать шестнадцатых.


Сокращение
Во втором примере полученную дробь можно сократить.
Что это значит? Обратите внимание – и числитель, и знаменатель этой дроби делятся на четыре. Разделить оба числа на общий делитель и называется – сократить дробь. Получим три четвертых.


Неправильные дроби
Но, предположим, мы умножили четыре на две пятых. Получилось восемь пятых. Это неправильная дробь.
Её обязательно нужно привести к правильному виду. Для это нужно выделить из нее целую часть.
Здесь нужно использовать деление с остатком. Получаем единицу и три в остатке.
Одна целая и три пятых и есть наша правильная дробь.
Привести к правильному виду тридцать пять восьмых – задача чуть посложнее.Самое близкое к тридцати семи число, которое делится на восемь – это тридцать два. При делении получим четыре. Отнимем от тридцати пяти тридцать два – получим три. Итог: четыре целых и три восьмых.


Равенство числителя и знаменателя. А тут все очень просто и красиво. При равенстве числителя и знаменателя получается просто единица.
Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.
Запишем сначала основное правило:
Определение 1
Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей a / b и c / d это можно выразить как a b · c d = a · c b · d .
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 1 4 и 1 8 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8 · 4 = 32). Соответственно, площадь каждого из них будет равна 1 32 от площади всей фигуры, т.е. 1 32 кв. единицы.
У нас получился закрашенный фрагмент со сторонами, равными 5 8 числовой единицы и 3 4 числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна 5 8 · 3 4 кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их 15 , значит, общая площадь составляет 15 32 квадратных единиц.
Поскольку 5 · 3 = 15 и 8 · 4 = 32 , мы можем записать следующее равенство:
5 8 · 3 4 = 5 · 3 8 · 4 = 15 32
Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как a b · c d = a · c b · d . Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Разберем решения нескольких задач на умножение обыкновенных дробей.
Пример 1
Умножьте 7 11 на 9 8 .
Решение
Для начала подсчитаем произведение числителей указанных дробей, умножив 7 на 9 . У нас получилось 63 . Затем вычислим произведение знаменателей и получим: 11 · 8 = 88 . Составим их двух чисел ответ: 63 88 .
Все решение можно записать так:
7 11 · 9 8 = 7 · 9 11 · 8 = 63 88
Ответ: 7 11 · 9 8 = 63 88 .
Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.
Пример 2
Вычислите произведение дробей 4 15 и 55 6 .
Решение
Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:
4 15 · 55 6 = 4 · 55 15 · 6 = 220 90
Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на 10 .
Выполним сокращение дроби: 220 90 НОД (220 , 90) = 10 , 220 90 = 220: 10 90: 10 = 22 9 . В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 22 9 = 2 4 9 .
Ответ: 4 15 · 55 6 = 2 4 9 .
Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду a · c b · d . Разложим значения переменных на простые множители и одинаковые из них сократим.
Поясним, как это выглядит, используя данные конкретной задачи.
Пример 3
Вычислите произведение 4 15 · 55 6 .
Решение
Запишем вычисления, исходя из правила умножения. У нас получится:
4 15 · 55 6 = 4 · 55 15 · 6
Поскольку как 4 = 2 · 2 , 55 = 5 · 11 , 15 = 3 · 5 и 6 = 2 · 3 , значит, 4 · 55 15 · 6 = 2 · 2 · 5 · 11 3 · 5 · 2 · 3 .
2 · 11 3 · 3 = 22 9 = 2 4 9
Ответ : 4 15 · 55 6 = 2 4 9 .
Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:
a b · c d = c d · a b = a · c b · d
Как перемножить обыкновенную дробь с натуральным числом
Запишем сразу основное правило, а потом попробуем объяснить его на практике.
Определение 2
Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби a b на натуральное число n можно записать в виде формулы a b · n = a · n b .
Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:
a b · n = a b · n 1 = a · n b · 1 = a · n b
Поясним нашу мысль конкретными примерами.
Пример 4
Вычислите произведение 2 27 на 5 .
Решение
В результате умножения числителя исходной дроби на второй множитель получим 10 . В силу правила, указанного выше, мы получим в результате 10 27 . Все решение приведено в этой записи:
2 27 · 5 = 2 · 5 27 = 10 27
Ответ: 2 27 · 5 = 10 27
Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.
Пример 5
Условие: вычислите произведение 8 на 5 12 .
Решение
По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что 5 12 · 8 = 5 · 8 12 = 40 12 . Итоговая дробь имеет признаки делимости на 2 , поэтому нам нужно выполнить ее сокращение:
НОК (40 , 12) = 4 , значит, 40 12 = 40: 4 12: 4 = 10 3
Теперь нам осталось только выделить целую часть и записать готовый ответ: 10 3 = 3 1 3 .
В этой записи можно видеть все решение целиком: 5 12 · 8 = 5 · 8 12 = 40 12 = 10 3 = 3 1 3 .
Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.
Ответ: 5 12 · 8 = 3 1 3 .
Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:
a b · n = n · a b = a · n b
Как выполнить умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.
Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Покажем на примере, как это делается.
Пример 6
Умножьте четыре обыкновенные дроби 1 20 , 12 5 , 3 7 и 5 8 .
Решение: для начала сделаем запись произведения. У нас получится 1 20 · 12 5 · 3 7 · 5 8 . Нам надо перемножить между собой все числители и все знаменатели: 1 20 · 12 5 · 3 7 · 5 8 = 1 · 12 · 3 · 5 20 · 5 · 7 · 8 .
Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.
1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 1 · (2 · 2 · 3) · 3 · 5 2 · 2 · 5 · 5 · 7 (2 · 2 · 2) = 3 · 3 5 · 7 · 2 · 2 · 2 = 9 280
Ответ: 1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 9 280 .
Пример 7
Перемножьте 5 чисел 7 8 · 12 · 8 · 5 36 · 10 .
Решение
Для удобства мы можем сгруппировать дробь 7 8 с числом 8 , а число 12 с дробью 5 36 , поскольку при этом нам будут очевидны будущие сокращения. В итоге у нас получится:
7 8 · 12 · 8 · 5 36 · 10 = 7 8 · 8 · 12 · 5 36 · 10 = 7 · 8 8 · 12 · 5 36 · 10 = 7 1 · 2 · 2 · 3 · 5 2 · 2 · 3 · 3 · 10 = = 7 · 5 3 · 10 = 7 · 5 · 10 3 = 350 3 = 116 2 3
Ответ: 7 8 · 12 · 8 · 5 36 · 10 = 116 2 3 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Умножение десятичных дробей происходит в три этапа.
Десятичные дроби записывают в столбик и умножают как обыкновенные числа.
Считаем количество знаков после запятой у первой десятичной дроби и у второй. Их количество складываем.
В полученном результате отсчитываем справа налево столько же цифр, сколько получилось их в пункте выше и ставим запятую.
Как умножать десятичные дроби
Записываем десятичные дроби в столбик и умножаем их как натуральные числа, не обращая внимания на запятые. То есть 3,11 мы рассматриваем как 311 , а 0,01 как 1 .
Получили 311 . Теперь считаем количество знаков (цифр) после запятой у обеих дробей. В первой десятичной дроби два знака и во второй - два. Общее количество цифр после запятых:
Отсчитываем справа налево 4 знака (цифры) у полученного числа. В полученном результате цифр меньше, чем нужно отделить запятой. В таком случае нужно слева приписать недостающее число нулей.
У нас не хватает одной цифры, поэтому приписываем слева один ноль.

При умножении любой десятичной дроби на 10; 100; 1000 и т.д. запятая в десятичной дроби перемещается вправо на столько знаков, сколько нулей стоит после единицы.
- 70,1 · 10 = 701
- 0,023 · 100 = 2,3
- 5,6 · 1 000 = 5 600
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т.д., надо в этой дроби перенести запятую влево на столько знаков, сколько нулей стоит перед единицей.
Считаем и ноль целых!
- 12 · 0,1 = 1,2
- 0,05 · 0,1 = 0,005
- 1,256 · 0,01 = 0,012 56
Умножение дробей
Умножение обыкновенных дробей рассмотрим в нескольких возможных вариантах.
Умножение обыкновенной дроби на дробь
Это наиболее простой случай, в котором нужно пользоваться следующими правилами умножения дробей .
Чтобы умножить дробь на дробь , надо:
- числитель первой дроби умножить на числитель второй дроби и их произведение записать в числитель новой дроби;
- знаменатель первой дроби умножить на знаменатель второй дроби и их произведение записать в знаменатель новой дроби;
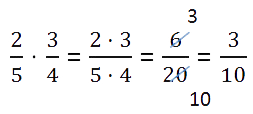
Прежде чем перемножать числители и знаменатели проверьте нельзя ли сократить дроби. Сокращение дробей при расчётах значительно облегчит ваши вычисления.

Умножение дроби на натуральное число
Чтобы дробь умножить на натуральное число нужно числитель дроби умножить на это число, а знаменатель дроби оставить без изменения.
Если в результате умножения получилась неправильная дробь, не забудьте превратить её в смешанное число, то есть выделить целую часть.

Умножение смешанных чисел
Чтобы перемножить смешанные числа, надо вначале превратить их в неправильные дроби и после этого умножить по правилу умножения обыкновенных дробей.

Другой способ умножения дроби на натуральное число
Иногда при расчётах удобнее воспользоваться другим способом умножения обыкновенной дроби на число.
Чтобы умножить дробь на натуральное число нужно знаменатель дроби разделить на это число, а числитель оставить прежним.

Как видно из примера, этим вариантом правила удобнее пользоваться, если знаменатель дроби делится без остатка на натуральное число.
Как умножить дробь на целое число правило
I. Чтобы умножить десятичную дробь на натуральное число, нужно умножить ее на это число, не обращая внимания на запятую, и в полученном произведении отделить запятой столько цифр справа, сколько их было после запятой в данной дроби.
Примеры. Выполнить умножение: 1) 1,25·7; 2) 0,345·8; 3) 2,391·14.
Решение.

II . Чтобы умножить одну десятичную дробь на другую, нужно выполнить умножение, не обращая внимания на запятые, и в полученном результате отделить запятой справа столько цифр, сколько их было после запятых в обоих множителях вместе.
Примеры. Выполнить умножение: 1) 18, 2·0,09; 2) 3,2·0,065; 3) 0,54·12,3.
Решение.

III. Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д. нужно перенести запятую вправо на 1, 2, 3 и т. д. цифр.
Примеры. Выполнить умножение: 1) 3,25·10; 2) 0,637·100; 3) 4,307·1000; 4) 2,04·1000; 5) 0,00031·10000.
Решение.

IV. Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д. нужно перенести запятую влево на 1, 2, 3 и т. д. цифр.
Примеры. Выполнить умножение: 1) 28,3·0,1; 2) 324,7·0,01; 3) 6,85·0,01; 4) 6179,5·0,001; 5) 92,1·0,0001.
www.mathematics-repetition.com
Умножение десятичных дробей, правила, примеры, решения.
Переходим к изучению следующего действия с десятичными дробями, сейчас мы всесторонне рассмотрим умножение десятичных дробей . Сначала обговорим общие принципы умножения десятичных дробей. После этого перейдем к умножению десятичной дроби на десятичную дробь, покажем, как выполняется умножение десятичных дробей столбиком, рассмотрим решения примеров. Дальше разберем умножение десятичных дробей на натуральные числа, в частности на 10, 100 и т.д. В заключение поговорим об умножении десятичных дробей на обыкновенные дроби и смешанные числа.
Сразу скажем, что в этой статье мы будем говорить лишь об умножении положительных десятичных дробей (смотрите положительные и отрицательные числа). Остальные случаи разобраны в статьях умножение рациональных чисел и умножение действительных чисел .
Навигация по странице.
Общие принципы умножения десятичных дробей
Обсудим общие принципы, которых следует придерживаться при проведении умножения с десятичными дробями.
Так как конечные десятичные дроби и бесконечные периодические дроби являются десятичной формой записи обыкновенных дробей, то умножение таких десятичных дробей по сути является умножением обыкновенных дробей. Иными словами, умножение конечных десятичных дробей , умножение конечной и периодической десятичных дробей , а также умножение периодических десятичных дробей сводится к умножению обыкновенных дробей после перевода десятичных дробей в обыкновенные.
Рассмотрим примеры применения озвученного принципа умножения десятичных дробей.
Выполните умножение десятичных дробей 1,5 и 0,75 .
Заменим умножаемые десятичные дроби соответствующими обыкновенными дробями. Так как 1,5=15/10 и 0,75=75/100 , то. Можно провести сокращение дроби, после чего выделить целую часть из неправильной дроби, а удобнее полученную обыкновенную дробь 1 125/1 000 записать в виде десятичной дроби 1,125 .
Следует отметить, что конечные десятичные дроби удобно умножать столбиком, об этом способе умножения десятичных дробей мы поговорим в следующем пункте.
Рассмотрим пример умножения периодических десятичных дробей.
Вычислите произведение периодических десятичных дробей 0,(3) и 2,(36) .
Выполним перевод периодических десятичных дробей в обыкновенные дроби:
Тогда. Можно полученную обыкновенную дробь перевести в десятичную дробь: 
Если среди умножаемых десятичных дробей присутствуют бесконечные непериодические, то все умножаемые дроби, в том числе конечные и периодические, следует округлить до некоторого разряда (смотрите округление чисел ), после чего выполнять умножение полученных после округления конечных десятичных дробей.
Выполните умножение десятичных дробей 5,382… и 0,2 .
Сначала округлим бесконечную непериодическую десятичную дробь, округление можно провести до сотых, имеем 5,382…≈5,38 . Конечную десятичную дробь 0,2 округлять до сотых нет необходимости. Таким образом, 5,382…·0,2≈5,38·0,2 . Осталось вычислить произведение конечных десятичных дробей: 5,38·0,2=538/100·2/10= 1 076/1 000=1,076 .
Умножение десятичных дробей столбиком
Умножение конечных десятичных дробей можно выполнять столбиком, аналогично умножению столбиком натуральных чисел.
Сформулируем правило умножения десятичных дробей столбиком . Чтобы умножить десятичные дроби столбиком, надо:
- не обращая внимания на запятые, выполнить умножение по всем правилам умножения столбиком натуральных чисел;
- в полученном числе отделить десятичной запятой столько цифр справа, сколько десятичных знаков в обоих множителях вместе, при этом если в произведении не хватает цифр, то слева нужно дописать нужное количество нулей.
Рассмотрим примеры умножения десятичных дробей столбиком.
Выполните умножение десятичных дробей 63,37 и 0,12 .
Проведем умножение десятичных дробей столбиком. Сначала умножаем числа, не обращая внимания на запятые: 
Осталось в полученном произведении поставить запятую. Ей нужно отделить 4 цифры справа, так как в множителях в сумме четыре десятичных знака (два в дроби 3,37 и два в дроби 0,12). Цифр там хватает, поэтому нулей слева дописывать не придется. Закончим запись: 
В итоге имеем 3,37·0,12=7,6044 .
Вычислите произведение десятичных дробей 3,2601 и 0,0254 .
Выполнив умножение столбиком без учета запятых, получаем следующую картину: 
Теперь в произведении нужно отделить запятой 8 цифр справа, так как общее количество десятичных знаков умножаемых дробей равно восьми. Но в произведении только 7 цифр, поэтому, нужно слева приписать столько нулей, чтобы можно было отделить запятой 8 цифр. В нашем случае нужно приписать два нуля: 
На этом умножение десятичных дробей столбиком закончено.
Умножение десятичных дробей на 0,1, 0,01, и т.д.
Довольно часто приходится умножать десятичные дроби на 0,1 , 0,01 и так далее. Поэтому целесообразно сформулировать правило умножения десятичной дроби на эти числа, которое следует из рассмотренных выше принципов умножения десятичных дробей.
Итак, умножение данной десятичной дроби на 0,1 , 0,01 , 0,001 и так далее дает дробь, которая получается из исходной, если в ее записи перенести запятую влево на 1 , 2 , 3 и так далее цифр соответственно, при этом если не хватает цифр для переноса запятой, то нужно слева дописать необходимое количество нулей.
Например, чтобы умножить десятичную дробь 54,34 на 0,1 , надо в дроби 54,34 перенести запятую влево на 1 цифру, при этом получится дробь 5,434 , то есть, 54,34·0,1=5,434 . Приведем еще один пример. Умножим десятичную дробь 9,3 на 0,0001 . Для этого нам нужно в умножаемой десятичной дроби 9,3 перенести запятую на 4 цифры влево, но запись дроби 9,3 не содержит такого количества знаков. Поэтому нам нужно в записи дроби 9,3 слева приписать столько нулей, чтобы можно было беспрепятственно осуществить перенос запятой на 4 цифры, имеем 9,3·0,0001=0,00093 .
Заметим, что озвученное правило умножения десятичной дроби на 0,1, 0,01, … справедливо и для бесконечных десятичных дробей. К примеру, 0,(18)·0,01=0,00(18) или 93,938…·0,1=9,3938… .
Умножение десятичной дроби на натуральное число
По своей сути умножение десятичных дробей на натуральные числа ничем не отличается от умножения десятичной дроби на десятичную дробь.
Конечную десятичную дробь умножать на натуральное число удобнее всего столбиком, при этом следует придерживаться правил умножения столбиком десятичных дробей, рассмотренных в одном из предыдущих пунктов.
Вычислите произведение 15·2,27 .
Проведем умножение натурального числа на десятичную дробь столбиком: 
При умножении периодической десятичной дроби на натуральное число, периодическую дробь следует заменить обыкновенной дробью.
Умножьте десятичную дробь 0,(42) на натуральное число 22 .
Сначала переведем периодическую десятичную дробь в обыкновенную дробь:
Теперь выполним умножение: . Этот результат в виде десятичной дроби имеет вид 9,(3) .
А при умножении бесконечной непериодической десятичной дроби на натуральное число нужно предварительно провести округление.
Выполните умножение 4·2,145… .
Округлив до сотых исходную бесконечную десятичную дробь, мы придем к умножению натурального числа и конечной десятичной дроби. Имеем 4·2,145…≈4·2,15=8,60 .
Умножение десятичной дроби на 10, 100, …
Довольно часто приходится умножать десятичные дроби на 10, 100, … Поэтому целесообразно подробно остановиться на этих случаях.
Озвучим правило умножения десятичной дроби на 10, 100, 1 000 и т.д. При умножении десятичной дроби на 10, 100, … в ее записи нужно перенести запятую вправо на 1, 2, 3, … цифры соответственно и отбросить лишние нули слева; если в записи умножаемой дроби не хватает цифр для переноса запятой, то нужно дописать необходимое количество нулей справа.
Умножьте десятичную дробь 0,0783 на 100 .
Перенесем в записи дроби 0,0783 на две цифры вправо, при этом получим 007,83 . Отбросив два нуля слева, получаем десятичную дробь 7,38 . Таким образом, 0,0783·100=7,83 .
Выполните умножение десятичной дроби 0,02 на 10 000 .
Чтобы умножить 0,02 на 10 000 , нам нужно перенести запятую на 4 цифры вправо. Очевидно, в записи дроби 0,02 не хватает цифр для переноса запятой на 4 цифры, поэтому допишем несколько нулей справа, чтобы можно было осуществить перенос запятой. В нашем примере достаточно дописать три нуля, имеем 0,02000 . После переноса запятой получим запись 00200,0 . Отбросив нули слева, имеем число 200,0 , которое равно натуральному числу 200 , оно и является результатом умножения десятичной дроби 0,02 на 10 000 .
Озвученное правило справедливо и для умножения бесконечных десятичных дробей на 10, 100, … При умножении периодических десятичных дробей нужно быть аккуратными с периодом дроби, которая является результатом умножения.
Умножьте периодическую десятичную дробь 5,32(672) на 1 000 .
Перед умножением распишем периодическую десятичную дробь как 5,32672672672… , это нам позволит не допустить ошибки. Теперь перенесем запятую вправо на 3 знака, имеем 5 326,726726… . Таким образом, после умножения получается периодическая десятичная дробь 5 326,(726) .
5,32(672)·1 000=5 326,(726) .
При умножении бесконечных непериодических дробей на 10, 100, … нужно предварительно провести округление бесконечной дроби до некоторого разряда, после чего проводить умножение.
Умножение десятичной дроби на обыкновенную дробь или смешанное число
Для умножения конечной десятичной дроби или бесконечной периодической десятичной дроби на обыкновенную дробь или смешанное число, нужно десятичную дробь представить в виде обыкновенной дроби, после чего провести умножение.
Проведите умножение десятичной дроби 0,4 на смешанное число.
Так как 0,4=4/10=2/5 и, то. Полученное число можно записать в виде периодической десятичной дроби 1,5(3) .
При умножении бесконечной непериодической десятичной дроби на обыкновенную дробь или смешанное число, обыкновенную дробь или смешанное число следует заменить десятичной дробью, после чего провести округление умножаемых дробей и закончить вычисления.
Так как 2/3=0,6666… , то. После округления умножаемых дробей до тысячных, приходим к произведению двух конечных десятичных дробей 3,568 и 0,667 . Выполним умножение в столбик: 
Полученный результат следует округлить до тысячных, так как умножаемые дроби были взяты с точностью до тысячных, имеем 2,379856≈2,380 .
www.cleverstudents.ru
Умножение обыкновенных дробей: правила, примеры, решения.
Продолжим изучать действия с обыкновенными дробями. Сейчас в центре внимания умножение обыкновенных дробей . В этой статье мы дадим правило умножения обыкновенных дробей, рассмотрим применение этого правила при решении примеров. Также остановимся на умножении обыкновенной дроби на натуральное число. В заключение рассмотрим, как проводится умножение трех и большего количества дробей.
Навигация по странице.
Умножение обыкновенной дроби на обыкновенную дробь
Начнем с формулировки правила умножения обыкновенных дробей : умножение дроби на дробь дает дробь, числитель которой равен произведению числителей умножаемых дробей, а знаменатель равен произведению знаменателей.
То есть, умножению обыкновенных дробей a/b и c/d отвечает формула .
Приведем пример, иллюстрирующий правило умножения обыкновенных дробей. Рассмотрим квадрат со стороной 1 ед. , при этом его площадь равна 1 ед 2 . Разделим этот квадрат на равные прямоугольники со сторонами 1/4 ед. и 1/8 ед. , при этом исходный квадрат будет состоять из 4·8=32 прямоугольников, следовательно, площадь каждого прямоугольника составляет 1/32 долю площади исходного квадрата, то есть, она равна 1/32 ед 2 . Теперь закрасим часть исходного квадрата. Все наши действия отражает рисунок ниже.

Стороны закрашенного прямоугольника равны 5/8 ед. и 3/4 ед. , значит, его площадь равна произведению дробей 5/8 и 3/4 , то есть, ед 2 . Но закрашенный прямоугольник состоит из 15 «маленьких» прямоугольников, значит, его площадь равна 15/32 ед 2 . Следовательно, . Так как 5·3=15 и 8·4=32 , то последнее равенство можно переписать как ![]() , что подтверждает формулу умножения обыкновенных дробей вида .
, что подтверждает формулу умножения обыкновенных дробей вида .
Заметим, что с помощью озвученного правила умножения можно умножать и правильные и неправильные дроби, и дроби с одинаковыми знаменателями, и дроби с разными знаменателями.
Рассмотрим примеры умножения обыкновенных дробей .
Выполните умножение обыкновенной дроби 7/11 на обыкновенную дробь 9/8 .
Произведение числителей умножаемых дробей 7 и 9 равно 63 , а произведение знаменателей 11 и 8 равно 88 . Таким образом, умножение обыкновенных дробей 7/11 и 9/8 дает дробь 63/88 .
Вот краткая запись решения: ![]() .
.
Не следует забывать про сокращение полученной дроби, если в результате умножения получается сократимая дробь, и про выделение целой части из неправильной дроби.
Выполните умножение дробей 4/15 и 55/6 .
Применим правило умножения обыкновенных дробей:  .
.
Очевидно, полученная дробь сократима (признак делимости на 10 позволяет утверждать, что числитель и знаменатель дроби 220/90 имеют общий множитель 10). Выполним сокращение дроби 220/90: НОД(220, 90)=10 и  . Осталось выделить целую часть из полученной неправильной дроби: .
. Осталось выделить целую часть из полученной неправильной дроби: .
Заметим, что сокращение дроби можно проводить до вычисления произведений числителей и произведений знаменателей умножаемых дробей, то есть, когда дробь имеет вид . Для этого числа a , b , c и d заменяются их разложениями на простые множители, после чего сокращаются одинаковые множители числителя и знаменателя.
Для пояснения, вернемся к предыдущему примеру.
Вычислите произведение дробей вида .
По формуле умножения обыкновенных дробей имеем ![]() .
.
Так как 4=2·2 , 55=5·11 , 15=3·5 и 6=2·3 , то ![]() . Теперь сокращаем общие простые множители:
. Теперь сокращаем общие простые множители: ![]() .
.
Остается лишь вычислить произведения в числителе и знаменателе, после чего выделить целую часть из неправильной дроби: ![]() .
.
Следует отметить, что для умножения дробей характерно переместительное свойство, то есть, умножаемые дроби можно менять местами: ![]() .
.
Умножение обыкновенной дроби на натуральное число
Начнем с формулировки правила умножения обыкновенной дроби на натуральное число : умножение дроби на натуральное число дает дробь, числитель которой равен произведению числителя умножаемой дроби на натуральное число, а знаменатель равен знаменателю умножаемой дроби.
С помощью букв правило умножения дроби a/b на натуральное число n имеет вид .
Формула следует из формулы умножения двух обыкновенных дробей вида . Действительно, представив натуральное число как дробь со знаменателем 1, получим ![]() .
.
Рассмотрим примеры умножения дроби на натуральное число.
Выполните умножение дроби 2/27 на 5 .
Умножение числителя 2 на число 5 дает 10 , поэтому в силу правила умножения дроби на натуральное число, произведение 2/27 на 5 равно дроби 10/27 .
Все решение удобно записывать так: ![]() .
.
При умножении дроби на натуральное число полученную дробь часто приходится сокращать, а если она еще и неправильная, то представлять ее в виде смешанного числа.
Умножьте дробь 5/12 на число 8 .
По формуле умножения дроби на натуральное число имеем  . Очевидно, полученная дробь сократима (признак делимости на 2 указывает на общий делитель 2 числителя и знаменателя). Выполним сокращение дроби 40/12: так как НОК(40, 12)=4 , то
. Очевидно, полученная дробь сократима (признак делимости на 2 указывает на общий делитель 2 числителя и знаменателя). Выполним сокращение дроби 40/12: так как НОК(40, 12)=4 , то  . Осталось выделить целую часть: .
. Осталось выделить целую часть: .
Вот все решение:  .
.
Отметим, что сокращение можно было провести, заменив числа в числителе и знаменателе их разложениями на простые множители. В этом случае решение выглядело бы так: .
В заключение этого пункта заметим, что умножение дроби на натуральное число обладает переместительным свойством, то есть, произведение дроби на натуральное число равно произведению этого натурального числа на дробь: ![]() .
.
Умножение трех и большего количества дробей
То, как мы определили обыкновенные дроби и действие умножение с ними, позволяет утверждать, что все свойства умножения натуральных чисел распространяются и на умножение дробей.
Переместительное и сочетательное свойства умножения позволяют однозначно определить умножение трех и большего количества дробей и натуральных чисел . При этом все происходит по аналогии с умножением трех и большего количества натуральных чисел. В частности, дроби и натуральные числа в произведении можно для удобства вычисления переставлять местами, а при отсутствии скобок, указывающих порядок выполнения действий, мы можем сами расставить скобки любым из допустимых способов.
Рассмотрим примеры умножения нескольких дробей и натуральных чисел.
Выполните умножение трех обыкновенных дробей 1/20 , 12/5 , 3/7 и 5/8 .
Запишем произведение, которое нам нужно вычислить ![]() . В силу правила умножения дробей записанное произведение равно дроби, числитель которой равен произведению числителей всех дробей, а знаменатель – произведению знаменателей:
. В силу правила умножения дробей записанное произведение равно дроби, числитель которой равен произведению числителей всех дробей, а знаменатель – произведению знаменателей: ![]() .
.
Прежде чем вычислить произведения в числителе и знаменателе, целесообразно заменить все множители их разложениями на простые множители и провести сокращение (можно, конечно, сократить дробь и после умножения, но во многих случаях это требует больших вычислительных усилий): .
![]() .
.
Выполните умножение пяти чисел ![]() .
.
В этом произведении удобно сгруппировать дробь 7/8 с числом 8 , а число 12 с дробью 5/36 , это позволит упростить вычисления, так как при такой группировке очевидно сокращение. Имеем
.
![]() .
.
www.cleverstudents.ru
Популярное:
- При обращении в районный суд Уважаемые посетители сайта! Управление Федерального казначейства по г. Санкт-Петербургу (Межрайонная ИФНС России №10 по Санкт-Петербургу) ИНН налогового органа Номер счета получателя СЕВЕРО-ЗАПАДНОЕ […]
- Расчет госпошлины на снижение размера алиментов Суды придерживаются следующей позиции: Госпошлина рассчитывается от суммы, на которую уменьшается размер алиментов (от цены иска). Пример расчета размера госпошлины в суд при […]
- Деление десятичных дробей, правила, примеры, решения. Продолжаем изучать действия с десятичными дробями, пришло время поговорить про деление десятичных дробей. Начнем с общих принципов деления десятичных дробей. Дальше […]
- Статья 333.19 НК РФ. Размеры государственной пошлины по делам, рассматриваемым Верховным Судом Российской Федерации, судами общей юрисдикции, мировыми судьями СТ 333.19 НК РФ. 1. По делам, рассматриваемым Верховным Судом […]
- Типовое положение о комиссии (уполномоченном) по социальному страхованию N 556а "Типовое положение о комиссии (уполномоченном) по социальному страхованию" УТВЕРЖДАЮ Председатель Фонда социального страхования Российской Федерации […]
- Изменились реквизиты для оплаты госпошлины ВС РФ, а также АС г. Москвы и АС Московского округа Опубликованы новые банковские реквизиты для уплаты госпошлины по рассматриваемым делам в ВС РФ, Арбитражном суде города Москвы и […]
- Коллектор в бурении-это Горная порода с высокой пористостью и проницаемостью, содержащая извлекаемые количества нефти и газа. Основными классификационными признаками коллектора являются условия фильтрации и аккумуляции в них […]
- Наша группа в ВК Получить Скидку на обучение. Успей получить скидку 1000 рублей! Запись в автошколу Заполните эту форму, мы свяжемся с Вами и пригласим Вас на занятия. Добро пожаловать! 1. Предупреждающие знаки Предупреждающие […]
В этой статье мы разберем умножение смешанных чисел . Сначала озвучим правило умножения смешанных чисел и рассмотрим применение этого правила при решении примеров. Дальше поговорим об умножении смешанного числа и натурального числа. Наконец, научимся выполнять умножение смешанного числа и обыкновенной дроби.
Навигация по странице.
Умножение смешанных чисел.
Умножение смешанных чисел можно свести к умножению обыкновенных дробей. Для этого достаточно выполнить перевод смешанных чисел в неправильные дроби.
Запишем правило умножения смешанных чисел :
- Во-первых, умножаемые смешанные числа нужно заменить неправильными дробями;
- Во-вторых, нужно воспользоваться правилом умножения дроби на дробь.
Рассмотрим примеры применения этого правила при умножении смешанного числа на смешанное число.
Выполните умножение смешанных чисел и .
Сначала представим умножаемые смешанные числа в виде неправильных дробей: ![]() и
и ![]() . Теперь мы можем умножение смешанных чисел заменить умножением обыкновенных дробей:
. Теперь мы можем умножение смешанных чисел заменить умножением обыкновенных дробей: ![]() . Применив правило умножения дробей, получаем
. Применив правило умножения дробей, получаем ![]() . Полученная дробь несократима (смотрите сократимые и несократимые дроби), но она неправильная (смотрите правильные и неправильные дроби), поэтому, для получения окончательного ответа осталось выполнить выделение целой части из неправильной дроби: .
. Полученная дробь несократима (смотрите сократимые и несократимые дроби), но она неправильная (смотрите правильные и неправильные дроби), поэтому, для получения окончательного ответа осталось выполнить выделение целой части из неправильной дроби: .
Запишем все решение в одну строку: .
 .
.
Для закрепления навыков умножения смешанных чисел рассмотрим решение еще одного примера.
Выполните умножение .
Смешные числа и равны соответственно дробям 13/5 и 10/9 . Тогда  . На этом этапе самое время вспомнить про сокращение дроби: заменим все числа в дроби их разложениями на простые множители, и выполним сокращение одинаковых множителей.
. На этом этапе самое время вспомнить про сокращение дроби: заменим все числа в дроби их разложениями на простые множители, и выполним сокращение одинаковых множителей.
Умножение смешанного числа и натурального числа
После замены смешанного числа неправильной дробью, умножение смешанного числа и натурального числа приводится к умножению обыкновенной дроби и натурального числа.
Выполните умножение смешанного числа и натурального числа 45 .
Смешанное число равно дроби , тогда ![]() . Заменим числа в полученной дроби их разложениями на простые множители, произведем сокращение, после чего выделим целую часть: .
. Заменим числа в полученной дроби их разложениями на простые множители, произведем сокращение, после чего выделим целую часть: .
 .
.
Умножение смешанного числа и натурального числа иногда удобно проводить с использованием распределительного свойства умножения относительно сложения. В этом случае произведение смешанного числа и натурального числа равно сумме произведений целой части на данное натуральное число и дробной части на данное натуральное число, то есть,  .
.
Вычислите произведение .
Заменим смешанное число суммой целой и дробной части, после чего применим распределительное свойство умножения: .
Умножение смешанного числа и обыкновенной дроби удобнее всего свести к умножению обыкновенных дробей, представив умножаемое смешанное число в виде неправильной дроби.
Умножьте смешанное число на обыкновенную дробь 4/15 .
Заменив смешанное число дробью , получаем  .
.
www.cleverstudents.ru
Умножение дробных чисел
§ 140. Определения . 1) Умножение дробного числа на целое определяется так же, как и умножение целых чисел, а именно: умножить какое-нибудь число (множимое) на целое число (множитель) – значит составить сумму одинаковых слагаемых, в которой каждое слагаемое равно множимому, а число слагаемых – множителю.
Так умножить на 5 – значит найти сумму:
2) Умножить какое-нибудь число (множимое) на дробь (множитель) значит найти эту дробь множимого.
Таким образом, нахождение дроби от данного числа, рассмотренное нами перед этим, мы будем теперь называть умножением на дробь.
3) Умножить какое-нибудь число (множимое) на смешанное число (множитель) – значит умножить множимое сперва на целое число множителя, потом на дробь множителя, и результаты этих двух умножений сложить между собой.
Например:
Число, получаемое после умножения, во всех этих случаях называется произведением , т. е. так же, как и при умножении целых чисел.
Из этих определений видно, что умножение дробных чисел есть действие всегда возможное и всегда однозначное.
§ 141. Целесообразность этих определений. Чтобы уяснить себе целесообразность введения в арифметику двух последних определений умножения, возьмем такую задачу:
Задача. Поезд, двигаясь равномерно проходит в час 40 км; как узнать, сколько километров пройдет этот поезд в данное число часов?
Если бы мы остались при том одном определении умножения, которое указывается в арифметике целых чисел (сложение равных слагаемых), то наша задача имела бы три различных решения, а именно:
Если данное число часов целое (например 5 часов), то для решения задачи надо 40 км умножить на это число часов.
Если данное число часов выражается дробью (например часа), то придется найти величину этой дроби от 40 км.
Наконец, если данное число часов смешанное (например часа), то надо будет 40 км умножить на целое число, заключающееся в смешанном числе, и к результату добавить еще такую дробь от 40 км, какая есть в смешанном числе.
Данные нами определения позволяют на все эти возможные случаи дать один общий ответ:
надо 40 км умножить на данное число часов, каково бы оно ни было.
Таким образом, если задачу представить в общем виде так:
Поезд, двигаясь равномерно, проходит в час v км. Сколько километров поезд пройдет в t часов?
то, какие бы ни были числа v и t, мы можем высказать один ответ: искомое число выражается формулой v · t.
Примечание. Найти какую-нибудь дробь данного числа, по нашему определению, означает то же самое, что умножить данное число на эту дробь; поэтому, например, найти 5% (т.е. пять сотых) данного числа означает то же самое, что умножить данное число на или на ; найти 125% данного числа означает то же, что умножить это число на или на , и т. д.
§ 142. Замечание о том, когда от умножения число увеличивается и когда оно уменьшается.
От умножения на правильную дробь число уменьшается, а от умножения на неправильную дробь число увеличивается, если эта неправильная дробь больше единицы, и остается без изменения, если она равна единице.
Замечание. При умножении дробных чисел, так же как и целых, произведение принимается равным нулю, если какой-нибудь из сомножителей равен нулю так, .
§ 143. Вывод правил умножения.
1) Умножение дроби на целое число. Пусть требуется дробь умножить на 5. Это значит увеличить в 5 раз. Чтобы увеличить дробь в 5 раз, достаточно увеличить ее числитель или уменьшить ее знаменатель в 5 раз (§ 127).
Поэтому:
Правило 1-е. Чтобы умножить дробь на целое число, надо умножить на это целое число числитель, а знаменатель оставить тот же; вместо этого можно также разделить на данное целое число знаменатель дроби (если это возможно), а числитель оставить тот же.
Замечание. Произведение дроби на ее знаменатель равно ее числителю.
Так:
Правило 2-е. Чтобы умножить целое число на дробь, надо умножить целое число на числитель дроби и это произведение сделать числителем, а знаменателем подписать знаменатель данной дроби.
Правило 3-е. Чтобы умножить дробь на дробь, надо умножить числитель на числитель и знаменатель на знаменатель и первое произведение сделать числителем, а второе знаменателем произведения.
Замечание. Это правило можно применять и к умножению дроби на целое число и целого числа на дробь, если только целое число будем рассматривать как дробь со знаменателем единица. Так:
Таким образом, изложенные сейчас три правила заключаются в одном, которое в общем виде можно выразить так:
4) Умножение смешанных чисел.
Правило 4-е. Чтобы умножить смешанные числа, надо обратить их в неправильные дроби и затем умножить по правилам умножения дробей
. Например:
§ 144. Сокращение при умножении
. При умножении дробей, если это возможно, надо делать предварительное сокращение, как это видно из следующих примеров:
Такое сокращение возможно делать потому, что величина дроби не изменится, если числитель и знаменатель ее будут уменьшены в одинаковое число раз.
§ 145. Изменение произведения с изменением сомножителей. Произведение дробных чисел при изменении сомножителей изменится совершенно так же, как и произведение целых чисел (§ 53), а именно: если увеличить (или уменьшить) какой-нибудь сомножитель в несколько раз, то и произведение увеличится (или уменьшится) во столько же раз.
Так, если в примере:
чтобы перемножить несколько дробей, надо перемножить их числители между собой и знаменатели между собой и первое произведение сделать числителем, а второе знаменателем произведения.
Замечание. Это правило можно применять и к таким произведениям, в которых некоторые множители числа целые или смешанные, если только целое число будем рассматривать как дробь, у которой знаменатель единица, а смешанные числа будем обращать в неправильные дроби. Например:
§ 147. Основные свойства умножения.
Те свойства умножения, которые были нами указаны для целых чисел (§ 56, 57, 59), принадлежат и умножению дробных чисел. Укажем эти свойства.
1) Произведение не изменяется от перемены мест сомножителей.
Например:
Действительно, согласно правилу предыдущего параграфа первое произведение равно дроби , а второе равно дроби . Но эти дроби одинаковы, потому что их члены отличаются только порядком целых сомножителей, а произведение целых чисел не изменяется при перемене мест сомножителей.
2) Произведение не изменится, если какую-либо группу сомножителей заменить их произведением.
Например:
Результаты получаются одинаковыми.
Из этого свойства умножения можно вывести такое заключение:
чтобы умножить какое-нибудь число на произведение, можно умножить это число на первый сомножитель, полученное число умножить на второй и т.д.
Например:
3) Распределительный закон умножения (относительно сложения). Чтобы умножить сумму на какое-нибудь число, можно умножить на это число каждое слагаемое отдельно и результаты сложить.
Закон этот был нами объяснен (§ 59) в применении к целым числам. Он остается верным без всяких изменений и для дробных чисел.
Покажем, в самом деле, что равенство
(a + b + c + .)m = am + bm + cm + .
(распределительный закон умножения относительно сложения) остается верным и тогда, когда буквы означают дробные числа. Рассмотрим три случая.
1) Предположим сначала, что множитель m есть число целое, например m = 3 (a, b, c – какие угодно числа). Согласно определению умножения на целое число можно написать (ограничиваясь для простоты тремя слагаемыми):
(a + b + c) * 3 = (a + b + c) + (a + b + c) + (a + b + c).
На основании сочетательного закона сложения мы можем в правой части опустить все скобки; применяя же переместительный закон сложения, а потом снова сочетательный, мы можем, очевидно, переписать правую часть так:
(a + a + a) + (b + b + b) + (c + c + c).
(a + b + c) * 3 = a * 3 + b * 3 + c * 3.
Значит, распределительный закон в этом случае подтверждается.
Умножение и деление дробей
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей»). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе - знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь - ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
По определению имеем:

Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные - и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
- Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить - тот, которому не нашлось пары;
- Если минусов не осталось, операция выполнена - можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение - весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей - это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Задача. Найдите значение выражения:
![]()
По определению имеем:

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Так делать нельзя!
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
Умножение дробей.
Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.
Умножение обыкновенной дроби на дробь.
Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.
Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.
Умножение дроби на число.
Для начала вспомним правило, любое число можно представить в виде дроби \(\bf n = \frac \) .
Воспользуемся этим правилом при умножении.
Неправильную дробь \(\frac = \frac = \frac + \frac = 2 + \frac = 2\frac \\\) перевели в смешанную дробь.
Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:
Умножение смешанных дробей.
Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.
Умножение взаимно обратных дробей и чисел.
Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.
Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.
Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.
Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.
Пример №1:
Вычислите произведение: а) \(\frac \times \frac \) б) \(\frac \times \frac \)
Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac \) б) \(\frac \times 11\)
Пример №3:
Напишите число обратное дроби \(\frac \)?
Ответ: \(\frac = 3\)
Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac \times \frac \)
Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?
Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac \) правильная, обратная ей дробь будет равна \(\frac \) – неправильная дробь. Ответ: нет.
б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac \) , обратная ей дробь равна \(\frac \). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.
в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac \), то обратная ей дробь будет \(\frac \). Дробь \(\frac \) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac = \frac = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.
Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac \) б) \(1\frac \times 3\frac \)
Решение:
а) \(4 \times 2\frac = \frac \times \frac = \frac = 11\frac \\\\ \)
б) \(1\frac \times 3\frac = \frac \times \frac = \frac = 4\frac \)
Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?
Рассмотрим на примере. Возьмем смешанную дробь \(1\frac \), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac = \frac \) . Обратная ей дробь будет равна \(\frac \) . Дробь \(\frac \) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Умножение десятичной дроби на натуральное число
Презентация к уроку
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
- В увлекательной форме ввести учащимся правило умножения десятичной дроби на натуральное число, на разрядную единицу и правило выражения десятичной дроби в процентах. Выработать умение применения полученных знаний при решении примеров и задач.
- Развивать и активизировать логическое мышление учащихся, умение выявлять закономерности и обобщать их, укреплять память, умение сотрудничать, оказывать помощь, оценивать свою работу и работу друг друга.
- Воспитывать интерес к математике, активность, мобильность, умение общаться.
Оборудование: интерактивная доска, плакат с цифрограммой, плакаты с высказываниями математиков.
- Организационный момент.
- Устный счёт – обобщение раннее изученного материала, подготовка к изучению нового материала.
- Объяснение нового материала.
- Задание на дом.
- Математическая физкультминутка.
- Обобщение и систематизация полученных знаний в игровой форме при помощи компьютера.
- Выставление оценок.
2. Ребята, сегодня у нас урок будет несколько необычным, потому что я буду проводить его не одна, а со своим другом. И друг у меня тоже необычный, сейчас вы его увидите. (На экране появляется компьютер-мультяшка). У моего друга есть имя и он умеет разговаривать. Как тебя зовут, дружок? Компоша отвечает: “Меня зовут Компоша”. Ты сегодня готов помогать мне? ДА! Ну тогда давай начнём урок.

Мне сегодня пришла зашифрованная цифрограмма, ребята, которую мы должны вместе решить и расшифровать. (На доске вывешивается плакат с устным счётом на сложение и вычитание десятичных дробей, в результате решения которого ребята получают следующий код 523914687. )

Расшифровать полученный код помогает Компоша. В результате расшифровки получается слово УМНОЖЕНИЕ. Умножение – это ключевое слово темы сегодняшнего урока. На мониторе высвечивается тема урока: “Умножение десятичной дроби на натуральное число”
Ребята, мы знаем, как выполняется умножение натуральных чисел. Сегодня мы с вами рассмотрим умножение десятичных чисел на натуральное число. Умножение десятичной дроби на натуральное число можно рассматривать как сумму слагаемых, каждое из которых равно этой десятичной дроби, а количество слагаемых равно этому натуральному числу. Например: 5,21 ·3 = 5,21 + 5, 21 + 5,21 = 15,63 Значит, 5,21 ·3 = 15,63. Представив 5,21 в виде обыкновенной дроби на натуральное число, получим
И в этом случае получили тот же результат 15,63. Теперь, не обращая внимания на запятую, возьмём вместо числа 5,21 число 521 и перемножим на данное натуральное число. Здесь мы должны помнить, что в одном из множителей запятая перенесена на два разряда вправо. При умножении чисел 5, 21 и3 получим произведение равное 15,63. Теперь в этом примере запятую перенесём влево на два разряда. Таким образом, во сколько раз один из множителей увеличили, во столько раз уменьшили произведение. На основании сходных моментов этих способов, сделаем вывод.

Чтобы умножить десятичную дробь на натуральное число, надо:
1) не обращая внимания на запятую, выполнить умножение натуральных чисел;
2) в полученном произведении отделить запятой справа столько знаков, сколько их в десятичной дроби.
На мониторе высвечиваются следующие примеры, которые мы разбираем вместе с Компошей и ребятами: 5,21 ·3 = 15,63 и 7,624 ·15 = 114,34. После показываю умножение на круглое число 12,6 ·50 = 630 . Далее перехожу на умножение десятичной дроби на разрядную единицу. Показываю следующие примеры: 7,423 ·100 = 742,3 и 5,2 ·1000 = 5200. Итак, ввожу правило умножения десятичной дроби на разрядную единицу:

Чтобы умножить десятичную дробь на разрядные единицы 10, 100, 1000 и т.д., надо в этой дроби перенести запятую вправо на столько знаков, сколько нулей в записи разрядной единицы.
Заканчиваю объяснение выражением десятичной дроби в процентах. Ввожу правило:

Чтобы выразить десятичную дробь в процентах, надо её умножить на 100 и приписать знак %.
Привожу пример на компьютере 0,5 ·100 = 50 или 0,5 = 50% .
4. По окончании объяснения даю ребятам домашнее задание, которое тоже высвечивается на мониторе компьютера: № 1030, № 1034, № 1032.

5. Чтобы ребята немного отдохнули, на закрепление темы делаем вместе с Компошей математическую физкультминутку. Все встают, показываю классу решённые примеры и они должны ответить, правильно или не правильно решён пример. Если пример решён правильно, то они поднимают руки над головой и делают хлопок ладонями. Если же пример решён не верно, ребята вытягивают руки в стороны и разминают пальчики.

6. А теперь вы немного отдохнули, можно и решить задания. Откройте учебник на странице 205, № 1029. в этом задании надо вычислить значение выражений:
Задания появляются на компьютере. По мере их решения, появляется картинка с изображением кораблика, который при полной сборке уплывает.

Решая это задание на компьютере, постепенно складывается ракета, решив последний пример, ракета улетает. Учитель делает небольшую информацию учащимся: “ Каждый год с казахстанской земли с космодрома Байконур взлетают к звёздам космические корабли. Рядом с Байконуром Казахстан строит свой новый космодром “Байтерек”.
Какое расстояние пройдёт легковая машина за 4 часа, если скорость легковой машины 74,8 км/ч.
Подарочный сертификат Не знаете, что подарить своей второй половинке, друзьям, сотрудникам, родственникам? Воспользуйтесь нашим специальным предложением: "Подарочный сертификат Дачного отеля "Синяя Осока". Сертификат дает […]
Продолжим изучать действия с обыкновенными дробями. Сейчас в центре внимания умножение обыкновенных дробей . В этой статье мы дадим правило умножения обыкновенных дробей, рассмотрим применение этого правила при решении примеров. Также остановимся на умножении обыкновенной дроби на натуральное число. В заключение рассмотрим, как проводится умножение трех и большего количества дробей.
Навигация по странице.
Умножение обыкновенной дроби на обыкновенную дробь
Начнем с формулировки правила умножения обыкновенных дробей : умножение дроби на дробь дает дробь, числитель которой равен произведению числителей умножаемых дробей, а знаменатель равен произведению знаменателей.
То есть, умножению обыкновенных дробей a/b и c/d отвечает формула .
Приведем пример, иллюстрирующий правило умножения обыкновенных дробей. Рассмотрим квадрат со стороной 1 ед. , при этом его площадь равна 1 ед 2 . Разделим этот квадрат на равные прямоугольники со сторонами 1/4 ед. и 1/8 ед. , при этом исходный квадрат будет состоять из 4·8=32 прямоугольников, следовательно, площадь каждого прямоугольника составляет 1/32 долю площади исходного квадрата, то есть, она равна 1/32 ед 2 . Теперь закрасим часть исходного квадрата. Все наши действия отражает рисунок ниже.

Стороны закрашенного прямоугольника равны 5/8 ед. и 3/4 ед. , значит, его площадь равна произведению дробей 5/8 и 3/4 , то есть, ед 2 . Но закрашенный прямоугольник состоит из 15 «маленьких» прямоугольников, значит, его площадь равна 15/32 ед 2 . Следовательно, . Так как 5·3=15 и 8·4=32 , то последнее равенство можно переписать как ![]() , что подтверждает формулу умножения обыкновенных дробей вида .
, что подтверждает формулу умножения обыкновенных дробей вида .
Заметим, что с помощью озвученного правила умножения можно умножать и правильные и неправильные дроби, и дроби с одинаковыми знаменателями, и дроби с разными знаменателями.
Рассмотрим примеры умножения обыкновенных дробей .
Выполните умножение обыкновенной дроби 7/11 на обыкновенную дробь 9/8 .
Произведение числителей умножаемых дробей 7 и 9 равно 63 , а произведение знаменателей 11 и 8 равно 88 . Таким образом, умножение обыкновенных дробей 7/11 и 9/8 дает дробь 63/88 .
Вот краткая запись решения: ![]() .
.
Не следует забывать про сокращение полученной дроби, если в результате умножения получается сократимая дробь, и про выделение целой части из неправильной дроби.
Выполните умножение дробей 4/15 и 55/6 .
Применим правило умножения обыкновенных дробей:  .
.
Очевидно, полученная дробь сократима (признак делимости на 10 позволяет утверждать, что числитель и знаменатель дроби 220/90 имеют общий множитель 10). Выполним сокращение дроби 220/90: НОД(220, 90)=10 и  . Осталось выделить целую часть из полученной неправильной дроби: .
. Осталось выделить целую часть из полученной неправильной дроби: .
Заметим, что сокращение дроби можно проводить до вычисления произведений числителей и произведений знаменателей умножаемых дробей, то есть, когда дробь имеет вид . Для этого числа a , b , c и d заменяются их разложениями на простые множители, после чего сокращаются одинаковые множители числителя и знаменателя.
Для пояснения, вернемся к предыдущему примеру.
Вычислите произведение дробей вида .
По формуле умножения обыкновенных дробей имеем ![]() .
.
Так как 4=2·2 , 55=5·11 , 15=3·5 и 6=2·3 , то ![]() . Теперь сокращаем общие простые множители:
. Теперь сокращаем общие простые множители: ![]() .
.
Остается лишь вычислить произведения в числителе и знаменателе, после чего выделить целую часть из неправильной дроби: ![]() .
.
Следует отметить, что для умножения дробей характерно переместительное свойство, то есть, умножаемые дроби можно менять местами: ![]() .
.
Умножение обыкновенной дроби на натуральное число
Начнем с формулировки правила умножения обыкновенной дроби на натуральное число : умножение дроби на натуральное число дает дробь, числитель которой равен произведению числителя умножаемой дроби на натуральное число, а знаменатель равен знаменателю умножаемой дроби.
С помощью букв правило умножения дроби a/b на натуральное число n имеет вид .
Формула следует из формулы умножения двух обыкновенных дробей вида . Действительно, представив натуральное число как дробь со знаменателем 1, получим ![]() .
.
Рассмотрим примеры умножения дроби на натуральное число.
Выполните умножение дроби 2/27 на 5 .
Умножение числителя 2 на число 5 дает 10 , поэтому в силу правила умножения дроби на натуральное число, произведение 2/27 на 5 равно дроби 10/27 .
Все решение удобно записывать так: ![]() .
.
При умножении дроби на натуральное число полученную дробь часто приходится сокращать, а если она еще и неправильная, то представлять ее в виде смешанного числа.
Умножьте дробь 5/12 на число 8 .
По формуле умножения дроби на натуральное число имеем  . Очевидно, полученная дробь сократима (признак делимости на 2 указывает на общий делитель 2 числителя и знаменателя). Выполним сокращение дроби 40/12: так как НОК(40, 12)=4 , то
. Очевидно, полученная дробь сократима (признак делимости на 2 указывает на общий делитель 2 числителя и знаменателя). Выполним сокращение дроби 40/12: так как НОК(40, 12)=4 , то  . Осталось выделить целую часть: .
. Осталось выделить целую часть: .
Вот все решение:  .
.
Отметим, что сокращение можно было провести, заменив числа в числителе и знаменателе их разложениями на простые множители. В этом случае решение выглядело бы так: .
В заключение этого пункта заметим, что умножение дроби на натуральное число обладает переместительным свойством, то есть, произведение дроби на натуральное число равно произведению этого натурального числа на дробь: ![]() .
.
Умножение трех и большего количества дробей
То, как мы определили обыкновенные дроби и действие умножение с ними, позволяет утверждать, что все свойства умножения натуральных чисел распространяются и на умножение дробей.
Переместительное и сочетательное свойства умножения позволяют однозначно определить умножение трех и большего количества дробей и натуральных чисел . При этом все происходит по аналогии с умножением трех и большего количества натуральных чисел. В частности, дроби и натуральные числа в произведении можно для удобства вычисления переставлять местами, а при отсутствии скобок, указывающих порядок выполнения действий, мы можем сами расставить скобки любым из допустимых способов.
Рассмотрим примеры умножения нескольких дробей и натуральных чисел.
Выполните умножение трех обыкновенных дробей 1/20 , 12/5 , 3/7 и 5/8 .
Запишем произведение, которое нам нужно вычислить ![]() . В силу правила умножения дробей записанное произведение равно дроби, числитель которой равен произведению числителей всех дробей, а знаменатель – произведению знаменателей:
. В силу правила умножения дробей записанное произведение равно дроби, числитель которой равен произведению числителей всех дробей, а знаменатель – произведению знаменателей: ![]() .
.
Прежде чем вычислить произведения в числителе и знаменателе, целесообразно заменить все множители их разложениями на простые множители и провести сокращение (можно, конечно, сократить дробь и после умножения, но во многих случаях это требует больших вычислительных усилий): .
![]() .
.
Выполните умножение пяти чисел ![]() .
.
В этом произведении удобно сгруппировать дробь 7/8 с числом 8 , а число 12 с дробью 5/36 , это позволит упростить вычисления, так как при такой группировке очевидно сокращение. Имеем
.
![]() .
.
Умножение дробей
Умножение обыкновенных дробей рассмотрим в нескольких возможных вариантах.
Умножение обыкновенной дроби на дробь
Это наиболее простой случай, в котором нужно пользоваться следующими правилами умножения дробей .
Чтобы умножить дробь на дробь , надо:
- числитель первой дроби умножить на числитель второй дроби и их произведение записать в числитель новой дроби;
- знаменатель первой дроби умножить на знаменатель второй дроби и их произведение записать в знаменатель новой дроби;
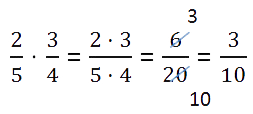
Прежде чем перемножать числители и знаменатели проверьте нельзя ли сократить дроби. Сокращение дробей при расчётах значительно облегчит ваши вычисления.

Умножение дроби на натуральное число
Чтобы дробь умножить на натуральное число нужно числитель дроби умножить на это число, а знаменатель дроби оставить без изменения.
Если в результате умножения получилась неправильная дробь, не забудьте превратить её в смешанное число, то есть выделить целую часть.

Умножение смешанных чисел
Чтобы перемножить смешанные числа, надо вначале превратить их в неправильные дроби и после этого умножить по правилу умножения обыкновенных дробей.

Другой способ умножения дроби на натуральное число
Иногда при расчётах удобнее воспользоваться другим способом умножения обыкновенной дроби на число.
Чтобы умножить дробь на натуральное число нужно знаменатель дроби разделить на это число, а числитель оставить прежним.

Как видно из примера, этим вариантом правила удобнее пользоваться, если знаменатель дроби делится без остатка на натуральное число.
Умножение смешанных чисел: правила, примеры, решения.
В этой статье мы разберем умножение смешанных чисел . Сначала озвучим правило умножения смешанных чисел и рассмотрим применение этого правила при решении примеров. Дальше поговорим об умножении смешанного числа и натурального числа. Наконец, научимся выполнять умножение смешанного числа и обыкновенной дроби.
Навигация по странице.
Умножение смешанных чисел.
Умножение смешанных чисел можно свести к умножению обыкновенных дробей. Для этого достаточно выполнить перевод смешанных чисел в неправильные дроби.
Запишем правило умножения смешанных чисел :
- Во-первых, умножаемые смешанные числа нужно заменить неправильными дробями;
- Во-вторых, нужно воспользоваться правилом умножения дроби на дробь.
Рассмотрим примеры применения этого правила при умножении смешанного числа на смешанное число.
Выполните умножение смешанных чисел и .
Сначала представим умножаемые смешанные числа в виде неправильных дробей: ![]() и
и ![]() . Теперь мы можем умножение смешанных чисел заменить умножением обыкновенных дробей:
. Теперь мы можем умножение смешанных чисел заменить умножением обыкновенных дробей: ![]() . Применив правило умножения дробей, получаем
. Применив правило умножения дробей, получаем ![]() . Полученная дробь несократима (смотрите сократимые и несократимые дроби), но она неправильная (смотрите правильные и неправильные дроби), поэтому, для получения окончательного ответа осталось выполнить выделение целой части из неправильной дроби: .
. Полученная дробь несократима (смотрите сократимые и несократимые дроби), но она неправильная (смотрите правильные и неправильные дроби), поэтому, для получения окончательного ответа осталось выполнить выделение целой части из неправильной дроби: .
Запишем все решение в одну строку: .
 .
.
Для закрепления навыков умножения смешанных чисел рассмотрим решение еще одного примера.
Выполните умножение .
Смешные числа и равны соответственно дробям 13/5 и 10/9 . Тогда  . На этом этапе самое время вспомнить про сокращение дроби: заменим все числа в дроби их разложениями на простые множители, и выполним сокращение одинаковых множителей.
. На этом этапе самое время вспомнить про сокращение дроби: заменим все числа в дроби их разложениями на простые множители, и выполним сокращение одинаковых множителей.
Умножение смешанного числа и натурального числа
После замены смешанного числа неправильной дробью, умножение смешанного числа и натурального числа приводится к умножению обыкновенной дроби и натурального числа.
Выполните умножение смешанного числа и натурального числа 45 .
Смешанное число равно дроби , тогда ![]() . Заменим числа в полученной дроби их разложениями на простые множители, произведем сокращение, после чего выделим целую часть: .
. Заменим числа в полученной дроби их разложениями на простые множители, произведем сокращение, после чего выделим целую часть: .
 .
.
Умножение смешанного числа и натурального числа иногда удобно проводить с использованием распределительного свойства умножения относительно сложения. В этом случае произведение смешанного числа и натурального числа равно сумме произведений целой части на данное натуральное число и дробной части на данное натуральное число, то есть,  .
.
Вычислите произведение .
Заменим смешанное число суммой целой и дробной части, после чего применим распределительное свойство умножения: .
Умножение смешанного числа и обыкновенной дроби удобнее всего свести к умножению обыкновенных дробей, представив умножаемое смешанное число в виде неправильной дроби.
Умножьте смешанное число на обыкновенную дробь 4/15 .
Заменив смешанное число дробью , получаем  .
.
Умножение дробных чисел
§ 140. Определения . 1) Умножение дробного числа на целое определяется так же, как и умножение целых чисел, а именно: умножить какое-нибудь число (множимое) на целое число (множитель) – значит составить сумму одинаковых слагаемых, в которой каждое слагаемое равно множимому, а число слагаемых – множителю.
Так умножить на 5 – значит найти сумму:
2) Умножить какое-нибудь число (множимое) на дробь (множитель) значит найти эту дробь множимого.
Таким образом, нахождение дроби от данного числа, рассмотренное нами перед этим, мы будем теперь называть умножением на дробь.
3) Умножить какое-нибудь число (множимое) на смешанное число (множитель) – значит умножить множимое сперва на целое число множителя, потом на дробь множителя, и результаты этих двух умножений сложить между собой.
Например:
Число, получаемое после умножения, во всех этих случаях называется произведением , т. е. так же, как и при умножении целых чисел.
Из этих определений видно, что умножение дробных чисел есть действие всегда возможное и всегда однозначное.
§ 141. Целесообразность этих определений. Чтобы уяснить себе целесообразность введения в арифметику двух последних определений умножения, возьмем такую задачу:
Задача. Поезд, двигаясь равномерно проходит в час 40 км; как узнать, сколько километров пройдет этот поезд в данное число часов?
Если бы мы остались при том одном определении умножения, которое указывается в арифметике целых чисел (сложение равных слагаемых), то наша задача имела бы три различных решения, а именно:
Если данное число часов целое (например 5 часов), то для решения задачи надо 40 км умножить на это число часов.
Если данное число часов выражается дробью (например часа), то придется найти величину этой дроби от 40 км.
Наконец, если данное число часов смешанное (например часа), то надо будет 40 км умножить на целое число, заключающееся в смешанном числе, и к результату добавить еще такую дробь от 40 км, какая есть в смешанном числе.
Данные нами определения позволяют на все эти возможные случаи дать один общий ответ:
надо 40 км умножить на данное число часов, каково бы оно ни было.
Таким образом, если задачу представить в общем виде так:
Поезд, двигаясь равномерно, проходит в час v км. Сколько километров поезд пройдет в t часов?
то, какие бы ни были числа v и t, мы можем высказать один ответ: искомое число выражается формулой v · t.
Примечание. Найти какую-нибудь дробь данного числа, по нашему определению, означает то же самое, что умножить данное число на эту дробь; поэтому, например, найти 5% (т.е. пять сотых) данного числа означает то же самое, что умножить данное число на или на ; найти 125% данного числа означает то же, что умножить это число на или на , и т. д.
§ 142. Замечание о том, когда от умножения число увеличивается и когда оно уменьшается.
От умножения на правильную дробь число уменьшается, а от умножения на неправильную дробь число увеличивается, если эта неправильная дробь больше единицы, и остается без изменения, если она равна единице.
Замечание. При умножении дробных чисел, так же как и целых, произведение принимается равным нулю, если какой-нибудь из сомножителей равен нулю так, .
§ 143. Вывод правил умножения.
1) Умножение дроби на целое число. Пусть требуется дробь умножить на 5. Это значит увеличить в 5 раз. Чтобы увеличить дробь в 5 раз, достаточно увеличить ее числитель или уменьшить ее знаменатель в 5 раз (§ 127).
Поэтому:
Правило 1-е. Чтобы умножить дробь на целое число, надо умножить на это целое число числитель, а знаменатель оставить тот же; вместо этого можно также разделить на данное целое число знаменатель дроби (если это возможно), а числитель оставить тот же.
Замечание. Произведение дроби на ее знаменатель равно ее числителю.
Так:
Правило 2-е. Чтобы умножить целое число на дробь, надо умножить целое число на числитель дроби и это произведение сделать числителем, а знаменателем подписать знаменатель данной дроби.
Правило 3-е. Чтобы умножить дробь на дробь, надо умножить числитель на числитель и знаменатель на знаменатель и первое произведение сделать числителем, а второе знаменателем произведения.
Замечание. Это правило можно применять и к умножению дроби на целое число и целого числа на дробь, если только целое число будем рассматривать как дробь со знаменателем единица. Так:
Таким образом, изложенные сейчас три правила заключаются в одном, которое в общем виде можно выразить так:
4) Умножение смешанных чисел.
Правило 4-е. Чтобы умножить смешанные числа, надо обратить их в неправильные дроби и затем умножить по правилам умножения дробей
. Например:
§ 144. Сокращение при умножении
. При умножении дробей, если это возможно, надо делать предварительное сокращение, как это видно из следующих примеров:
Такое сокращение возможно делать потому, что величина дроби не изменится, если числитель и знаменатель ее будут уменьшены в одинаковое число раз.
§ 145. Изменение произведения с изменением сомножителей. Произведение дробных чисел при изменении сомножителей изменится совершенно так же, как и произведение целых чисел (§ 53), а именно: если увеличить (или уменьшить) какой-нибудь сомножитель в несколько раз, то и произведение увеличится (или уменьшится) во столько же раз.
Так, если в примере:
чтобы перемножить несколько дробей, надо перемножить их числители между собой и знаменатели между собой и первое произведение сделать числителем, а второе знаменателем произведения.
Замечание. Это правило можно применять и к таким произведениям, в которых некоторые множители числа целые или смешанные, если только целое число будем рассматривать как дробь, у которой знаменатель единица, а смешанные числа будем обращать в неправильные дроби. Например:
§ 147. Основные свойства умножения.
Те свойства умножения, которые были нами указаны для целых чисел (§ 56, 57, 59), принадлежат и умножению дробных чисел. Укажем эти свойства.
1) Произведение не изменяется от перемены мест сомножителей.
Например:
Действительно, согласно правилу предыдущего параграфа первое произведение равно дроби , а второе равно дроби . Но эти дроби одинаковы, потому что их члены отличаются только порядком целых сомножителей, а произведение целых чисел не изменяется при перемене мест сомножителей.
2) Произведение не изменится, если какую-либо группу сомножителей заменить их произведением.
Например:
Результаты получаются одинаковыми.
Из этого свойства умножения можно вывести такое заключение:
чтобы умножить какое-нибудь число на произведение, можно умножить это число на первый сомножитель, полученное число умножить на второй и т.д.
Например:
3) Распределительный закон умножения (относительно сложения). Чтобы умножить сумму на какое-нибудь число, можно умножить на это число каждое слагаемое отдельно и результаты сложить.
Закон этот был нами объяснен (§ 59) в применении к целым числам. Он остается верным без всяких изменений и для дробных чисел.
Покажем, в самом деле, что равенство
(a + b + c + .)m = am + bm + cm + .
(распределительный закон умножения относительно сложения) остается верным и тогда, когда буквы означают дробные числа. Рассмотрим три случая.
1) Предположим сначала, что множитель m есть число целое, например m = 3 (a, b, c – какие угодно числа). Согласно определению умножения на целое число можно написать (ограничиваясь для простоты тремя слагаемыми):
(a + b + c) * 3 = (a + b + c) + (a + b + c) + (a + b + c).
На основании сочетательного закона сложения мы можем в правой части опустить все скобки; применяя же переместительный закон сложения, а потом снова сочетательный, мы можем, очевидно, переписать правую часть так:
(a + a + a) + (b + b + b) + (c + c + c).
(a + b + c) * 3 = a * 3 + b * 3 + c * 3.
Значит, распределительный закон в этом случае подтверждается.
Деление дроби на натуральное число
Разделы: Математика
Тип урока: ОНЗ (открытие новых знаний – по технологии деятельностного метода обучения).
- Вывести приемы деления дроби на натуральное число;
- Сформировать способность к выполнению деления дроби на натуральное число;
- Повторить и закрепить деление дробей;
- Тренировать способность к сокращению дробей, анализу и решению задач.
Оборудование демонстрационный материал:
1. Задания для актуализации знаний:
![]()

2. Пробное (индивидуальное) задание.
1. Выполните деление:
2. Выполните деление, не выполняя всю цепочку вычислений: .
- При делении дроби на натуральное число можно умножить на это число знаменатель, а числитель оставить прежним.

- Если числитель делится на натуральное число, то при делении дроби на это число можно числитель разделить на число, а знаменатель оставить прежним.

I. Мотивация (самоопределение) к учебной деятельности.
- Организовать актуализацию требований к ученику со стороны учебной деятельности («надо»);
- Организовать деятельность учащихся по установке тематических рамок («могу»);
- Создать условия для возникновения у ученика внутренней потребности включения в учебную деятельность («хочу»).
Организация учебного процесса на этапе I.
Здравствуйте! Я рада видеть вас всех на уроке математики. Надеюсь, это взаимно.
Ребята, какие новые знания вы приобрели на прошлом уроке? (Делить дроби).
Верно. Что вам помогает выполнять деление дробей? (Правило, свойства).
Где эти знания нам необходимы? (В примерах, уравнениях, задачах).
Молодцы! Вы хорошо справились с заданиями на прошлом уроке. Хотите и сегодня открыть сами новые знания? (Да).
Тогда – в путь! А девизом урока возьмём высказывание «Математику нельзя изучать, наблюдая, как это делает сосед!».
II. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.
- Организовать актуализацию изученных способов действий, достаточных для построения нового знания. Зафиксировать эти способы вербально (в речи) и знаково (эталон) и обобщить их;
- Организовать актуализацию мыслительных операций и познавательных процессов, достаточных для построения нового знания;
- Мотивировать к пробному действию и его самостоятельному выполнению и обоснованию;
- Предъявить индивидуальное задание для пробного действия и проанализировать его с целью выявления нового учебного содержания;
- Организовать фиксацию образовательной цели и темы урока;
- Организовать выполнение пробного действия и фиксацию затруднения;
- Организовать анализ полученных ответов и зафиксировать индивидуальные затруднения в выполнении пробного действия или его обоснования.
Организация учебного процесса на этапе II.
Фронтально, с использованием планшетов (индивидуальных досок).
1. Сравните выражения:
![]() (Эти выражения равны)
(Эти выражения равны)
Что интересного вы заметили? (Числитель и знаменатель делимого, числитель и знаменатель делителя в каждом выражении увеличились в одно и то же число раз. Т.о., делимые и делители в выражениях представлены дробями, равными между собой).
Найдите значение выражения и запишите на планшете. (2)
Как записать это число в виде дроби?
Как вы выполнили действие деления? (Дети проговаривают правило, учитель вывешивает на доску буквенные обозначения)

2. Вычислите и запишите только результаты:
3. Сложите полученные результаты и запишите ответ. (2)
Как называется число, полученное в задании 3? (Натуральное)
Как вы думаете, сможете ли дробь разделить на натуральное число? (Да, постараемся)
Попробуйте это выполнить.
4. Индивидуальное (пробное) задание.
Выполните деление: (только пример а)

По какому правилу вы выполнили деление? (По правилу деления дроби на дробь)
А теперь разделите дробь на натуральное число более простым способом, не выполняя всю цепочку вычислений: (пример б). Даю вам на это 3 секунды.
У кого не получилось выполнить задание за 3 секунды?
У кого получилось? (Нет таких)
Почему? (Не знаем способа)
Что получили? (Затруднение)
А как вы думаете, чем мы будем заниматься на уроке? (Делить дроби на натуральные числа)
Верно, откройте тетради и запишите тему урока «Деление дроби на натуральное число».
Почему эта тема звучит как новая, ведь вы уже умеете делить дроби? (Нужен новый способ)
Верно. Сегодня установим приём, упрощающий деление дроби на натуральное число.
III. Выявление места и причины затруднения.
- Организовать восстановление выполненных операций и зафиксировать (вербальную и знаковую) место – шага, операции, где возникло затруднение;
- Организовать соотнесение действий учащихся с используемым способом (алгоритмом) и фиксирование во внешней речи причины затруднения – тех конкретных знаний, умений или способностей, которых недостает для решения исходной задачи такого типа.
Организация учебного процесса на этапе III.
Какое задание вы должны были выполнить? (Разделить дробь на натуральное число, не проделывая всю цепочку вычислений)
Что вызвало у вас затруднение? (Не смогли решить за короткое время быстрым способом)
Какую цель мы ставим перед собой на уроке? (Найти быстрый способ деления дроби на натуральное число)
Что вам поможет? (Уже известное правило деления дробей)
IV. Построение проекта выхода из затруднения.
- Уточнение цели проекта;
- Выбор способа (уточнение);
- Определение средств (алгоритм);
- Построение плана достижения цели.
Организация учебного процесса на этапе IV.
Вернёмся к пробному заданию. Вы сказали, что делили по правилу деления дробей? (Да)
Для этого заменили натуральное число дробью? (Да)
Какой шаг (или шаги), на ваш взгляд, можно пропустить?
(На доске открыта цепочка решения: 
Проанализируйте и сделайте вывод. (Шаг 1)
Если нет ответа, то подводим через вопросы:
Куда попал натуральный делитель? (В знаменатель)
Числитель изменился при этом? (Нет)
Так какой шаг можно «опустить»? (Шаг 1)
- Умножить знаменатель дроби на натуральное число.
- Числитель не изменяем.
- Получаем новую дробь.
V. Реализация построенного проекта.
- Организовать коммуникативное взаимодействие с целью реализации построенного проекта, направленного на приобретение недостающих знаний;
- Организовать фиксацию построенного способа действия в речи и знаков (с помощью эталона);
- Организовать решение исходной задачи и зафиксировать преодоление затруднения;
- Организовать уточнение общего характера нового знания.
Организация учебного процесса на этапе V.
А теперь выполните пробный пример новым способом быстро.
Теперь вы смогли выполнить задание быстро? (Да)
Объясните, как вы это сделали? (Дети проговаривают)
Значит, мы получили новое знание: правило деления дроби на натуральное число.
Молодцы! Проговорите его в парах.
Затем один ученик проговаривает классу. Фиксируем правило-алгоритм словесно и в виде эталона на доске.
Введите теперь буквенные обозначения и запишите формулу для нашего правила.

Ученик записывает на доске, проговаривая правило: при делении дроби на натуральное число можно умножить на это число знаменатель, а числитель оставить прежним.
(Все пишут формулу в тетрадях).
А теперь ещё раз проанализируйте цепочку решения пробного задания, обратив особое внимание на ответ. Что сделали? (Числитель дроби 15 разделили (сократили) на число 3)
Что это за число? (Натуральное, делитель)
Так как еще можно разделить дробь на натуральное число? (Проверить: если числитель дроби делится на это натуральное число, то можно числитель разделить на это число, результат записать в числитель новой дроби, а знаменатель оставить прежним)
Запишите этот способ в виде формулы. (Ученик записывает на доске проговаривая правило. Все записывают формулу в тетрадях.)

Вернёмся к первому способу. Можно им пользоваться в случае, если a:n? (Да, это общий способ)
А когда второй способ удобно применять? (Когда числитель дроби делится на натуральное число без остатка)
VI. Первичное закрепление с проговариванием во внешней речи.
- Организовать усвоение детьми нового способа действий при решении типовых задач с их проговариванием во внешней речи (фронтально, в парах или группах).
Организация учебного процесса на этапе VI.
Вычисли новым способом:
- №363 (а; г) – выполняют у доски, проговаривая правило.
- №363 (д; е) – в парах с проверкой по образцу.
VII. Самостоятельная работа с самопроверкой по эталону.
- Организовать самостоятельное выполнение учащимися задания на новый способ действия;
- Организовать самопроверку на основе сопоставления с эталоном;
- По результатам выполнения самостоятельной работы организовать рефлексию усвоения нового способа действия.
Организация учебного процесса на этапе VII.
Вычисли новым способом:
Учащиеся проверяют по эталону, отмечают правильность выполнения. Анализируются причины ошибок и ошибки исправляются.
Учитель спрашивает тех учащихся, кто допустил ошибки, в чём причина?
На этом этапе важно, чтобы каждый учащийся самостоятельно проверил свою работу.
Перед решением задания 8) рассмотреть пример из учебника:

IX. Рефлексия учебной деятельности на уроке.
- Организовать фиксацию нового содержания, изученного на уроке;
- Организовать рефлексивный анализ учебной деятельности с точки зрения выполнения требований, известных учащимся;
- Организовать оценивание учащимися собственной деятельности на уроке;
- Организовать фиксацию неразрешённых затруднений на уроке как направления будущей учебной деятельности;
- Организовать обсуждение и запись домашнего задания.
Организация учебного процесса на этапе IX.
Ребята, какое новое знание вы сегодня открыли? (Научились делить дробь на натуральное число простым способом)
Сформулируйте общий способ. (Говорят)
Каким способом, и в каких случаях можно пользоваться ещё? (Говорят)
В чём преимущество нового способа?
Достигли ли мы поставленной нами цели урока? (Да)
Какие знания вы использовали для достижения цели? (Говорят)
Всё ли у вас получилось?
В чём были затруднения?
